Design of Information Feedback Firefly Algorithm with a Nested Deep Learning Model for Intelligent Gesture Recognition of Visually Disabled People

Abstract

Gesture recognition is a developing topic in current technologies. The focus is to detect human gestures by utilizing mathematical methods for human–computer interaction. Some modes of human–computer interaction are touch screens, keyboard, mouse, etc. All these gadgets have their merits and demerits while implementing versatile hardware in computers. Gesture detection is one of the vital methods to construct user-friendly interfaces. Generally, gestures are created from any bodily state or motion but typically originate from the hand or face. Therefore, this manuscript designs an Information Feedback Firefly Algorithm with Nested Deep Learning (IFBFFA-NDL) model for intelligent gesture recognition of visually disabled people. The presented IFBFFA-NDL technique exploits the concepts of DL with a metaheuristic hyperparameter tuning strategy for the recognition process. To generate a collection of feature vectors, the IFBFFA-NDL technique uses the NASNet model. For optimal hyperparameter selection of the NASNet model, the IFBFFA algorithm is used. To recognize different types of gestures, a nested long short-term memory classification model was used. For exhibiting the improvised gesture detection efficiency of the IFBFFA-NDL technique, a detailed comparative result analysis was conducted and the outcomes highlighted the improved recognition rate of the IFBFFA-NDL technique as 99.73% compared to recent approaches.

Main article text

INTRODUCTION

Presently, human–machine communication is crucial for operating the machines remotely by the commands that are obtained from humans ( Gangrade and Bharti, 2023). From this perspective, gestures play a vital role in operating the machine at distant modes. The machines captured the gestures from humans and detected them to operate the machines ( Varsha and Nair, 2021). The gestures can be in different kinds of modes, such as dynamic and static. Gestures are categorized as static or dynamic. A dynamic gesture aims to change over a period and a static gesture remains unchanged over time ( Jindal et al., 2023). This project highlights the detection of static gestures. The automatic detection of hand gestures may have application in different areas like virtual reality design, sign language, and robotics ( Wu et al., 2023). The main issue is how to make a computer understand hand gestures.

Hand gestures change in orientation of the shape of hands and fingers ( Adeel et al., 2022). Therefore, non-linearity is one feature of hand gestures that should be dealt with. It is done through the metadata and content data carried by the images ( Zhang and Zeng, 2022). The metadata of hand gesture imageries is utilized for detecting the gestures. The process is the incorporation of two tasks: classification and feature extraction. Prior to the detection of any gesture, the attributes of an image should be derived. Any classification technique must be implemented after extracting those features ( Deepa et al., 2023). Therefore, the main problem is how to abstract those features and infer those attributes for classification ( Can et al., 2021). Vast features are essential for recognition and classification. Classical approaches for pattern detection cannot process natural datasets in raw form. Then, enormous efforts are needed for extracting features from raw data and they are not automated. CNN, a class of DL neural networks, can abstract attributes on the fly and fully connected layers are utilized for classification ( Al-Hammadi et al., 2020). CNN combines these two steps to decrease the computational complexity and memory requirements and offers superior performance. It can understand the nonlinear and complicated relationship among the images ( Kraljević et al., 2020). Hence, CNN-based methods will be leveraged to solve the problem.

This manuscript designs an Information Feedback Firefly Algorithm with Nested Deep Learning (IFBFFA-NDL) model for intelligent gesture recognition. The presented IFBFFA-NDL technique uses the NASNet model for feature extraction purposes. For optimal hyperparameter selection of the NASNet model, the IFBFFA algorithm is used. To recognize different types of gestures, a nested long short-term memory (NLSTM) classification model was used. For exhibiting the improvised gesture detection efficiency of the IFBFFA-NDL technique, a detailed comparative result analysis is carried out.

LITERATURE REVIEW

Ehrnsperger et al. (2020) investigated naïve gesture detection models and related new and conventional ML techniques. The accounted gestures are plain human gestures like hand swiping or foot kicking. For comparison, the models are evaluated regarding their TPR, FPR, real-time capacity along with the essential calculation power, and employment on low-price hardware. In Wang et al. (2020), the authors present a new model for uninterrupted hand gesture identification established on a frequency-modulated continuous wave radar. Initially, a 2D-FFT was used for assessing the Doppler and range parameters of the hand gesture raw information and building the DTM and RTM.

Kocejko et al. (2020) proposed a simple construction of a neural network for classifying hand gestures. This classifies the previously computed EMG signal parameters. The major objective of this study was to build a plain resolution that does not involve convolutional calculations and can be employed in microprocessors in low-price 3D-printed prosthetic arms. The dataset EMG signals similar to five diverse gestures are formed as part of the study. In Jo and Oh (2020), the authors aimed to vigorously detect hand gestures in real time by employing CRNN with overlapping windows and preprocessing. CRNN is a deep learning method that incorporates LSTM for time-sequence data classification and CNN for feature extraction. Köpüklü et al. (2019) presented a ranking scheme allowing offline-working CNN construction for operating effectively online by employing the sliding window technique. The presented construction comprises two methods: first, a lightweight CNN-constructed detector for recognizing gestures and secondly, a deep CNN for the classification of the identified gestures.

Sun et al. (2019) presented a region-based deep CNN (R-DCNN) for identifying and classifying gestures calculated by a frequency-modulated uninterrupted wave radar scheme. Micro-Doppler gesture signs are utilized, and the resultant spectrograms are given to the NN. This study is the first in utilizing R-DCNN for radar-based gesture detection through which several gestures can be routinely identified and classified without physically cutting the data streams based on every hand displacement priorly. In Bastos et al. (2019), the authors developed MLRRN, a multi-task established model that achieves both the identification and temporal recognition of gestures together. This also implements a dual loss function that takes into consideration the assignment of every video frame to a gesture class and decides the interval of frame related to every gesture. This technique counts with dual input, collecting data from human poses and appearances on the frames, along with residual modules and bidirectional recurrent layers.

THE PROPOSED IFBFFA-NDL TECHNIQUE

In this manuscript, we have focused on the development of an automated gesture recognition model, named the IFBFFA-NDL model. The presented IFBFFA-NDL technique exploits the concepts of DL with a metaheuristic hyperparameter tuning strategy for the recognition process. It involves three processes such as NASNet feature extraction, IFBFFA-based parameter tuning, and NLSTM-based recognition. Figure 1 represents the workflow of the IFBFFA-NDL approach.

Figure 1:

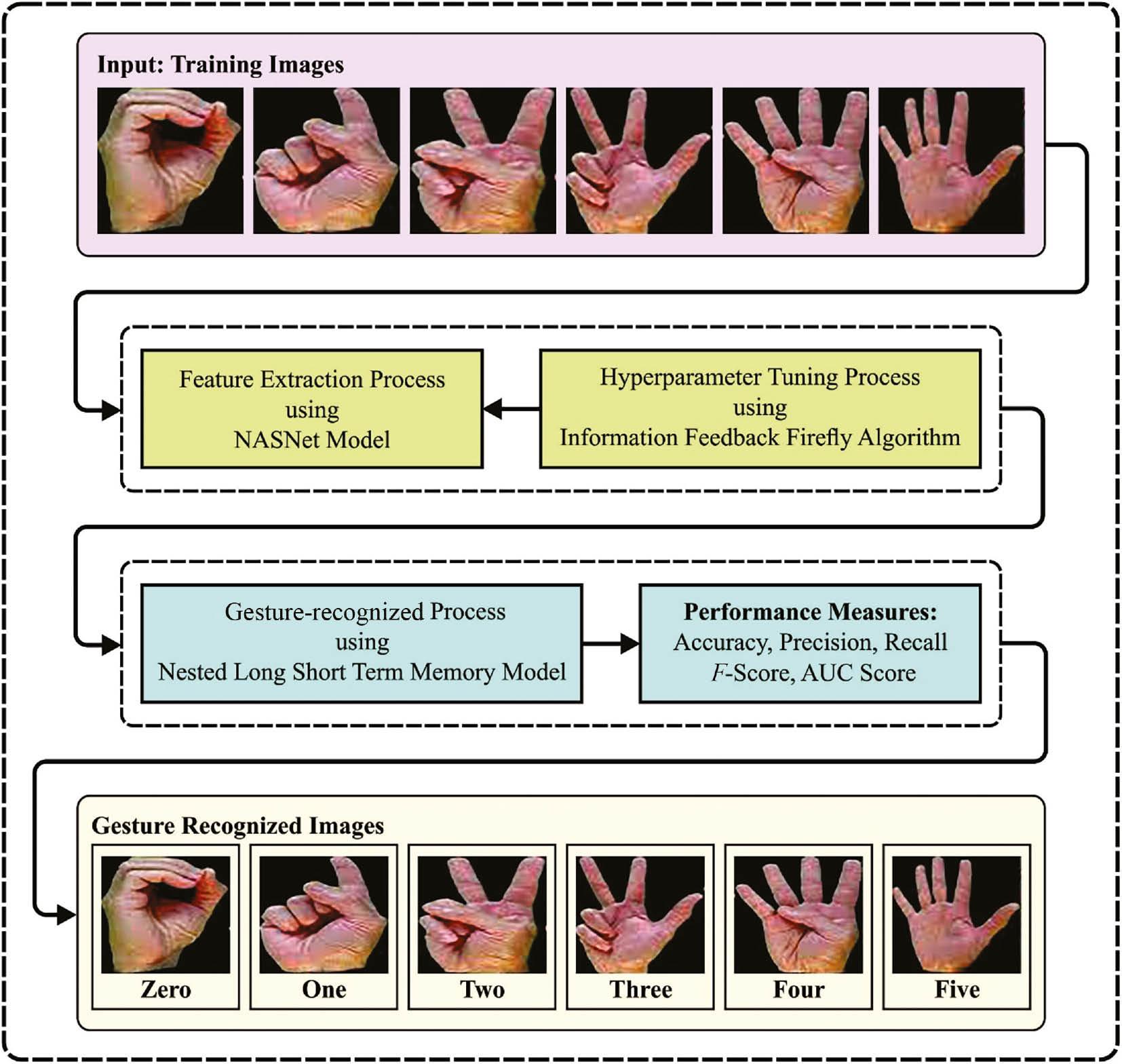
Workflow of the IFBFFA-NDL approach. IFBFFA-NDL, Information Feedback Firefly Algorithm with Nested Deep Learning.

The suggested technique is put under simulation by employing Python 3.6.5 tool on PC i5-8600k, 250GB SSD, GeForce 1050Ti 4GB, 16GB RAM, and 1TB HDD. The setups of the parameter are as follows: learning rate: 0.01, activation: ReLU, epoch count: 50, dropout: 0.5, and size of batch: 5.

Optimal feature extraction module

To generate a collection of feature vectors, the IFBFFA-NDL technique uses the NASNet model. NASNet is a neural architecture search network, a set of methods that can be devised automatically by learning the architectures of the method directly on the data of interest ( Kogilavani et al., 2022). Depending on the variations in the efficiency of the child block, the network adjustment can be made. The cell structure performance can be improved by carrying out reinforcement mutations and enhancing the child’s objective functions. A block is a small component, and a cell integrates numerous blocks. The data type determined the count of blocks and cells that are not fixed. Mapping, convolutions, pooling, and other processes are performed within a block. NASNet is one technique utilized to detect noninfected and infected patients due to its transferable learning approach. It presents more possibilities with a minimum network model.

For optimal hyperparameter selection of the NASNet model, the IFBFFA algorithm is used. FFA is the metaheuristic approach inspired by collective intelligence that can be utilized for resolving complicated optimization issues ( Mosavvar and Ghaffari, 2019). Initially, amounts of artificial fireflies are distributed at random. Then, all the fireflies emit light whose concentration fits the optimum level of the point where the firefly is positioned. The firefly with a lesser light intensity was absorbed by the firefly with more light. β absorption of fireflies is evaluated by using the following equation.

(1) $$\beta \mathrm{(}r)={\beta }_0{e}^{-\gamma r^2}$$

In Eq. (1), β, γ, and r represent the predetermined absorption, light absorption coefficient, and the distance between ith and jth fireflies, correspondingly. The distance between ith and jth fireflies at X _I and X _j is measured using the following formula:

(2) $$r=\sqrt{{\displaystyle \sum _{k=1}^d{\mathrm{(}{x}_{ik}-x_{jk})}^2}}.$$

The movement of ith firefly and their attraction to jth fireflies that are brighter are evaluated using Eq. (3):

(3) $$x_i=x_i+{\beta }_0{e}^{-\gamma r^2}\mathrm{(}{x}_j-x_i)+\alpha \left(rand-\frac{1}{2}\right)\hspace{0.17em},$$

where β ₀ denotes the degree of attraction and absorption of the light source. The γ value ranges in the interval [0, ∞] are defined by the variation in absorption. The second sentence shows the attraction and the third sentence is a randomizer that can be performed by α parameter within standard distribution [0, 1] as explain in Algorithm 1.

Algorithm 1

Pseudocode of FFA

Nomenclature

$$\text{U}i=i\text{th}$$ firefly, iε [1, n];

n = amount of fireflies;

max_ generation = total amount of generations of fireflies;

I i = Light intensity magnitude of the ith objective function (OF) ( x);

γ = absorption coefficient;

f( x i ) = Object function of ith firefly that is based on the position of d-dimension.

Produce S particles to comprise K randomly designated CHS

Firefly algorithm

Start

Initialize Parameter:

MaxGen: the maximal amount of generations

OF off ( x), where x = ( x l ,…, x d ) T

Produce early population of firefly or x i = ( i = 1,2,…, n)

Define the light intensity of I i at x i through f( x i )

While ( t < MaxGen)

For i = 1 to n (each n firefly);

For j = 1 to n (each n firefly)

If ( Ij > Ii), move ith firefly toward jth firefly;

End if Attractiveness differs with distance r through $$e^{-\gamma r^2}$$ ;

Compute novel solutions and upgrade light concentration;

End for j;

End for i;

Rank the firefly and search for the optimum outcome;

End while;

Postprocess outcomes and visualization;

End

In the IFBFFA algorithm, an information feedback mode was introduced to integrate helpful data from prior iterations into the update mechanism, which results in a considerable development in the solution quality ( Jiang et al., 2023).

Through weighted summation, this model produces a novel individual by integrating the data from a prior generation of individuals. The fixed model and random mode are the two operational models in the information feedback model. To avoid a dramatic expansion in model complexity emerging from the retention of excessive generations of population data, the number of selected prior individuals generally does not exceed three generations. The study focuses only on the case if the number of predecessors was 1.

(4) $$x_i^{t+1}=\alpha x_j^t+\beta y_i^{t+1}\hspace{0.17em}$$

(5) $$\alpha =\frac{f_i^{t+1}}{f_i^{t+1}+f_j^t},\beta =\frac{f_j^t}{f_i^{t+1}+f_j^t}\hspace{0.17em}$$

Consider the present generation as t + 1, then,

$$x_j^t$$ indicates the location of jth flamingo of the prior generation, $$y_i^{t+1}$$ shows that intermediate individuals can be derived by the FSA, $$x_i^{t+1}$$ denotes the location of ith flamingo of a similar generation, and f represents the fitness of the corresponding individuals. The initial one is if j = i, which is a fixed mode. The next is if = rand (1,2,…, N) which can be a randomized model. Dissimilar ways of j have dissimilar facilitation impacts.

Dissimilar choices of the parameter j might lead to dissimilar kinds of information feedback modes. Every two approaches for choosing j has its disadvantages and advantages, and one algorithm is not exactly superior to the others. The random mode could improve the learning possibility for outstanding individuals in the population and has better randomness, thus improving the global search ability of the model. Nonetheless, the random model might lead to a weakened precision and convergence rate before the model reaches local optima compared to the facilitation effect of the fixed model.

The study presents an information feedback method related to adaptive fitness adjustment and is applied to the FSA model. Based on the current fitness value the model chooses the suitable information feedback model dynamically. The performance can be improved by integrating the strength of two dissimilar models.

For dynamically modifying the method depending on fitness, the subsequent formula is modeled as a threshold.

(6) $$\sigma =\left|\frac{f_i^{t+1}-f_i^t}{f^t\text{max\hspace{0.17em}}-f^t\text{min\hspace{0.17em}}}\right|$$

Consider the present generation as t + 1, where

$$f_i^t$$ denotes the fitness value of the ith individual flamingo of the prior generation, $$f_i^{t+1}$$ signifies the location of the ith individual flamingo of the existing generation, and f ^t min and f ^t max represent the minimal and maximal fitness values of the prior generation, correspondingly.

Initially, every individual tends to have discrete distribution. Thus, it is worthwhile to set the feedback mode as fixed to improve the early optimization ability of the algorithm. As the algorithm continued to iterate, once the value evaluated by Eq. (6) is lesser than the critical value set before (10 ⁻⁴), then a better parameter was tested with dissimilar values attained by comparing the outcomes, which shows that the model can easily get stuck in a local optima. Individuals in the population randomly learn from the prior generation once the feedback mode is changed to a random model that is beneficial to discover the best location. During the updating process, the magnitude value is critical to select a suitable method, and by comparing outcomes of dissimilar test functions, the parameter size can be defined.

Nested DL-based recognition module

To recognize different types of gestures, the NLSTM classification model is exploited. NLSTM model is a kind of RNN with different levels of memory ( Islam et al., 2023). NLSTM is a nested together LSTM unit, unlike stacked LSTM. Owing to its features of generalization power and good robustness, NLSTM can be used in varied fields. NLSTM explores the inherent temporal feature in the input for capturing higher-level features. In NLSTM, the operation of memory cells can be imitated by typical LSTM cells. Likewise, NLSTM creates a temporal hierarchy of memory and could immediately access the inner memory; however, it exploits a selection process for long-term data that is only applicable. Figure 2 demonstrates the architecture of LSTM.

Figure 2:

Architecture of LSTM.

(7) $${\tilde{i}}_t={\tilde{\sigma }}_i\left({\tilde{x}}_t{\tilde{W}}_{xi}+{\tilde{h}}_{t-1}{\tilde{w}}_{hi}+{\tilde{b}}_i\right),$$

(8) $${\tilde{f}}_t={\tilde{\sigma }}_f\left({\tilde{x}}_t{\tilde{W}}_{xf}+{\tilde{h}}_{t-1}{\tilde{w}}_{hf}+{\tilde{b}}_f\right)\hspace{0.17em}$$

(9) $${\tilde{o}}_t={\tilde{\sigma }}_o\left({\tilde{x}}_t{\tilde{W}}_{xo}+{\tilde{h}}_{t-1}{\tilde{w}}_{ho}+{\tilde{b}}_o\right)\hspace{0.17em}$$

(10) $${\tilde{c}}_t={\tilde{f}}_t\odot {\tilde{c}}_{t-1}+{\tilde{i}}_t\odot {\tilde{\sigma }}_c\left({\tilde{x}}_t{\tilde{W}}_{xc}+{\tilde{h}}_{t-1}{\tilde{w}}_{hc}+{\tilde{b}}_c\right)\hspace{0.17em}$$

(11) $${\tilde{h}}_t={\tilde{o}}_t\odot {\tilde{\sigma }}_c\mathrm{(}{\tilde{c}}_t)\hspace{0.17em}$$

(12) $${\tilde{x}}_t=i_t\odot {\sigma }_C\mathrm{(}{x}_t{W}_{xc}+h_{t-1}{W}_{hc}+b_C)$$

(13) $${\tilde{h}}_{t-1}=f_t\odot {\tilde{c}}_{t-1},$$

where

$${\tilde{c}}_t$$ denotes the cell input state of the inner LSTM unit; $$\hspace{0.17em}{\tilde{i}}_t,{\tilde{f}}_t$$ and $${\tilde{o}}_t$$ indicate the states of three gates of inner LSTM; σ characterizes the activation function; $${\tilde{h}}_t,{\tilde{x}}_t$$ , and $${\tilde{h}}_{t-1}$$ show the input of the inner LSTM; $${\tilde{w}}_{hi},{\tilde{w}}_{hf},{\tilde{w}}_{ho}$$ and $${\tilde{w}}_{hc}$$ signify the corresponding weight vector between $${\tilde{h}}_{t-1}$$ to every gate and the cell input, x _t and h _t−1 represent the input of the outer LSTM; $${\tilde{W}}_{xf},{\tilde{W}}_{xi},$$ $${\tilde{W}}_{xo}$$ and $${\tilde{W}}_{xc}$$ indicate the corresponding weight vector between $${\tilde{x}}_t$$ to each gate and the cell inputs; $$\hspace{0.17em}\odot$$ epitomizes the scalar product of two vectors; and $${\widetilde{\hspace{0.17em}b}}_i,{\tilde{b}}_f,{\tilde{b}}_o$$ and $${\tilde{b}}_c$$ stand for the biases of every gate and the cell inputs.

(14) $$c_t={\tilde{h}}_t,\hspace{0.17em}$$

where

$${\tilde{h}}_t$$ denotes the output of the inner LSTM unit.

EXPERIMENTAL VALIDATION

The proposed model is simulated using Python tool. The gesture recognition results of the IFBFFA-NDL method are tested on the dataset, encompassing 2000 samples and 10 classes as illustrated in Table 1.

Table 1:

Details of database.

Digits	No. of count
0	200
1	200
2	200
3	200
4	200
5	200
6	200
7	200
8	200
9	200
Total number of count	2000

Figure 3 portrays the classifier outcomes of the IFBFFA-NDL approach under the test database. Figure 3a and b shows the confusion matrix offered by the IFBFFA-NDL model on 70:30 of TRP/TSP. The result signified that the IFBFFA-NDL method has identified and categorized all 10 class labels accurately. Likewise, Figure 3c exhibits the PR study of the IFBFFA-NDL approach. The result stated that the IFBFFA-NDL model has achieved higher PR performance under 10 classes. Eventually, Figure 3d shows the ROC study of the IFBFFA-NDL method. The result portrayed that the IFBFFA-NDL model has productive outcomes with higher ROC values under 10 class labels.

Figure 3:

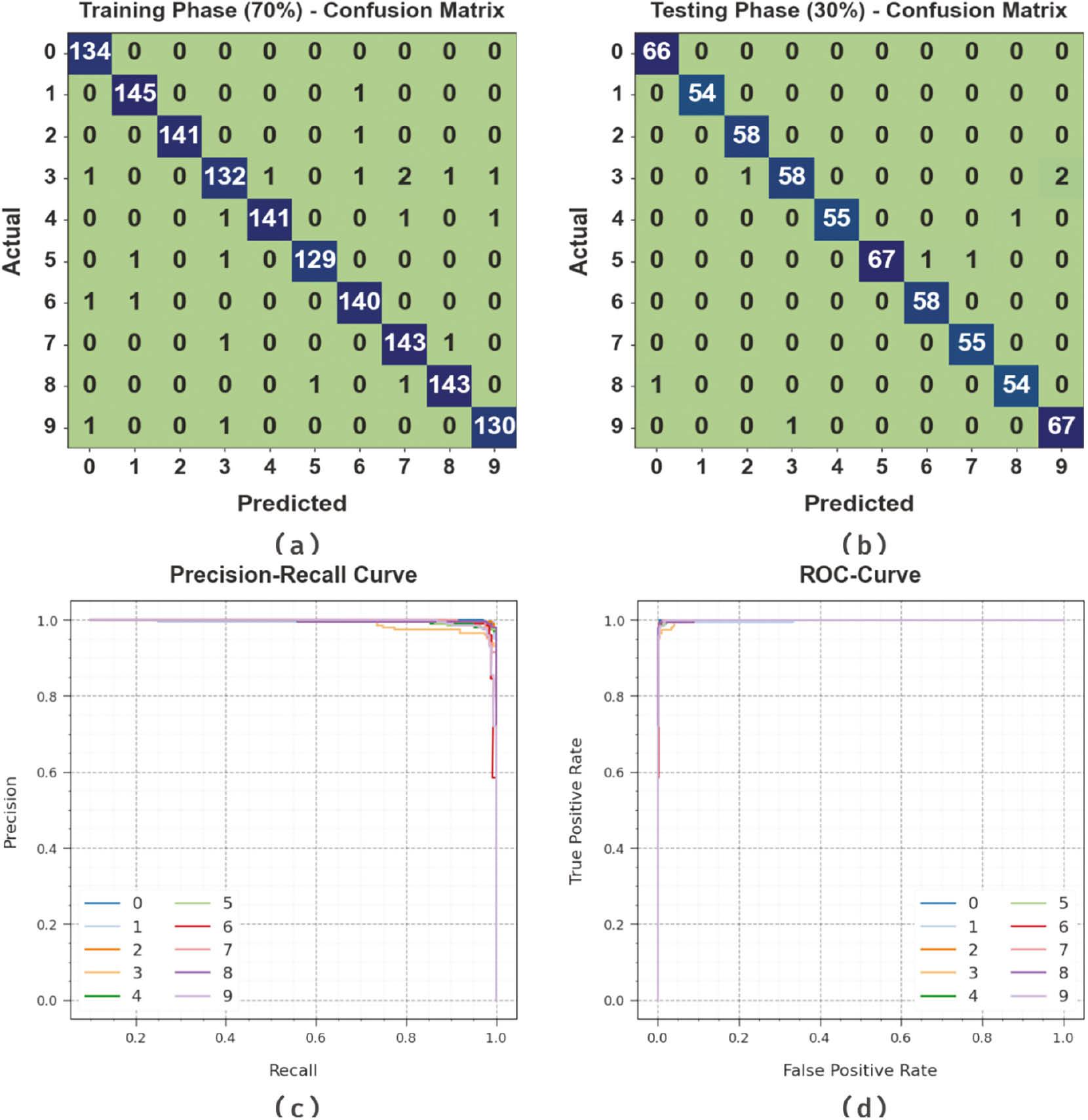
Classifier outcome of the IFBFFA-NDL system: (a-b) Confusion matrices, (c) PR-curve, and (d) ROC-curve. IFBFFA-NDL, Information Feedback Firefly Algorithm with Nested Deep Learning.

The overall gesture recognition results of the IFBFFA-NDL method are revealed in Table 2 and Figure 4. The outcomes identified that the IFBFFA-NDL algorithm reaches an effectual recognition rate under all classes. For instance, with 70% of TRP, the IFBFFA-NDL system provides average accu _y , prec _n , reca _l , F _score , and AUC _score of 99.69, 98.43, 98.43, 98.43, and 99.13%, respectively. Meanwhile, with 30% of TSP, the IFBFFA-NDL technique provides average accu _y , prec _n , reca _l , F _score , and AUC _score of 99.73, 98.69, 98.71, 98.69, and 99.28%, respectively.

Table 2:

Gesture recognition outcome of the IFBFFA-NDL approach on 70:30 of TRP/TSP.

Class	Accuracy	Precision	Recall	F-score	AUC score
Training phase (70%)
0	99.79	97.81	100.00	98.89	99.88
1	99.79	98.64	99.32	98.98	99.58
2	99.93	100.00	99.30	99.65	99.65
3	99.21	97.06	94.96	96.00	97.32
4	99.71	99.30	97.92	98.60	98.92
5	99.79	99.23	98.47	98.85	99.20
6	99.64	97.90	98.59	98.25	99.18
7	99.57	97.28	98.62	97.95	99.15
8	99.71	98.62	98.62	98.62	99.23
9	99.71	98.48	98.48	98.48	99.16
Average	99.69	98.43	98.43	98.43	99.13
Testing phase (30%)
0	99.83	98.51	100.00	99.25	99.91
1	100.00	100.00	100.00	100.00	100.00
2	99.83	98.31	100.00	99.15	99.91
3	99.33	98.31	95.08	96.67	97.45
4	99.83	100.00	98.21	99.10	99.11
5	99.67	100.00	97.10	98.53	98.55
6	99.83	98.31	100.00	99.15	99.91
7	99.83	98.21	100.00	99.10	99.91
8	99.67	98.18	98.18	98.18	99.00
9	99.50	97.10	98.53	97.81	99.08
Average	99.73	98.69	98.71	98.69	99.28

IFBFFA-NDL, Information Feedback Firefly Algorithm with Nested Deep Learning.

Figure 4:

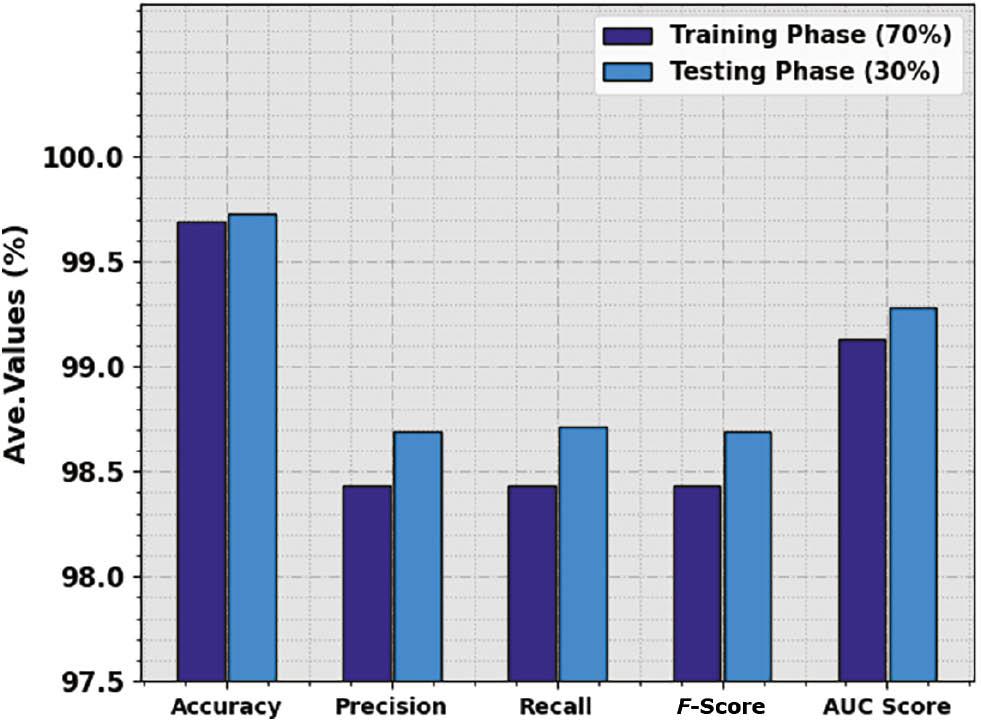
Average outcome of the IFBFFA-NDL approach on 70:30 of TRP/TSP. IFBFFA-NDL, Information Feedback Firefly Algorithm with Nested Deep Learning.

Figure 5 inspects the accuracy of the IFBFFA-NDL method in the training and validation of the test dataset. The result specified that the IFBFFA-NDL technique attained higher accuracy values over greater epochs. As well, the greater validation accuracy over training accuracy highlighted that the IFBFFA-NDL methodology learns productively on the test database.

Figure 5:

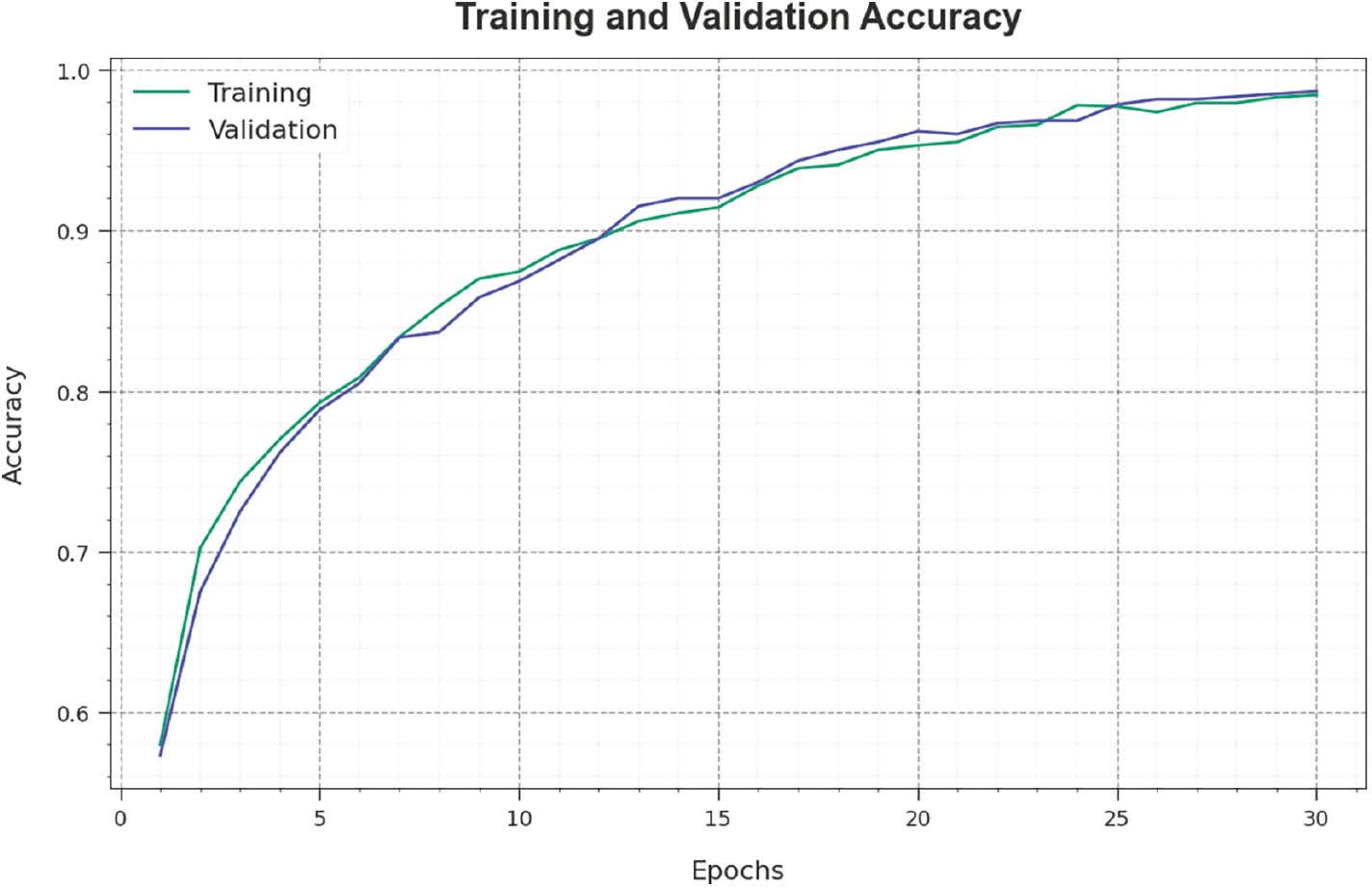
Accuracy curve of the IFBFFA-NDL approach. IFBFFA-NDL, Information Feedback Firefly Algorithm with Nested Deep Learning.

The loss analysis of the IFBFFA-NDL technique in training and validation is shown on the test database in Figure 6. The results highlighted that the IFBFFA-NDL technique attained adjacent values of training and validation loss. The IFBFFA-NDL method learns productively on a test database.

Figure 6:

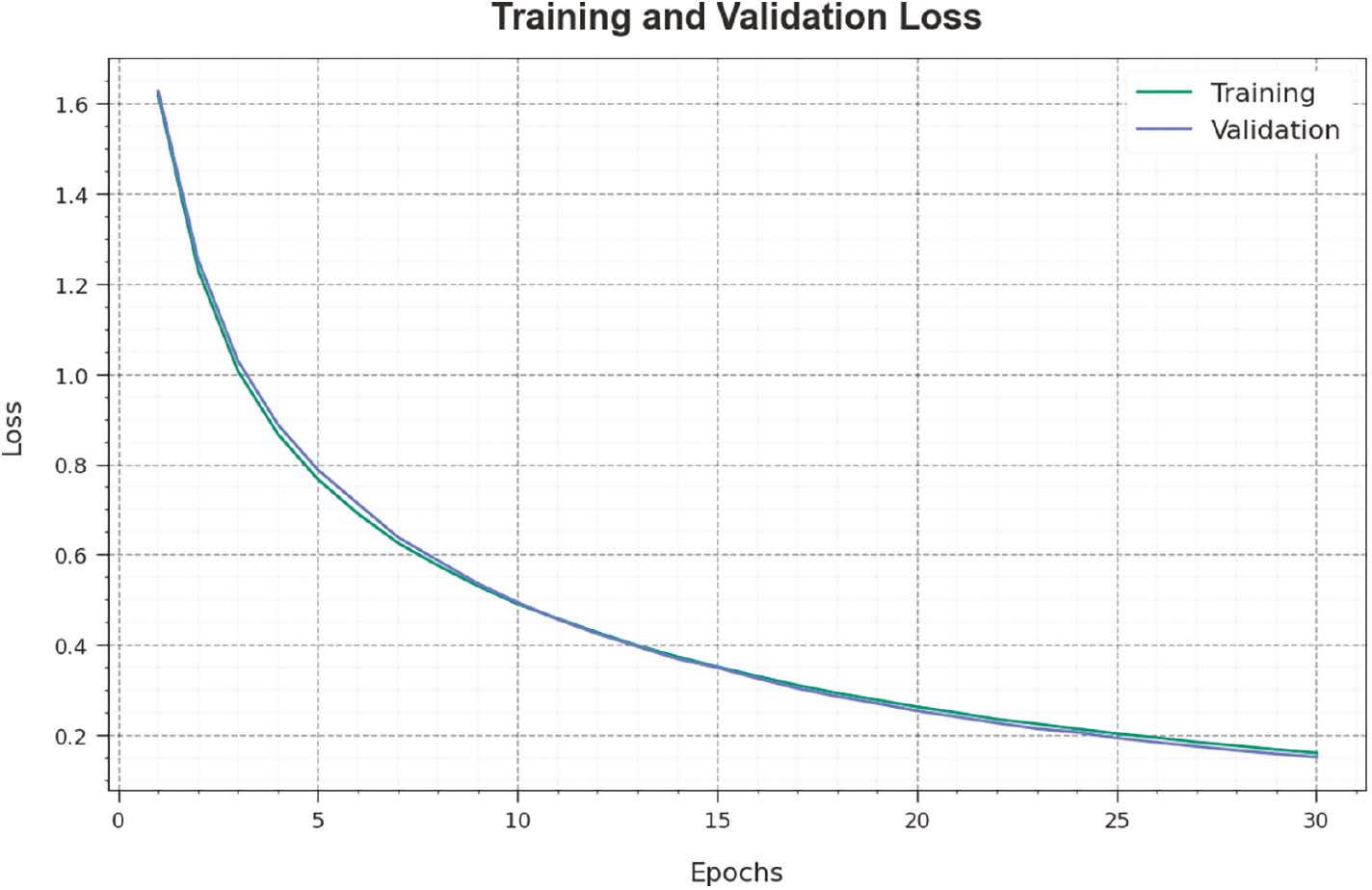
Loss curve of the IFBFFA-NDL approach. IFBFFA-NDL, Information Feedback Firefly Algorithm with Nested Deep Learning.

In Table 3 and Figure 7, the overall recognition outcomes of the IFBFFA-NDL approach are compared with current approaches ( Ozcan and Basturk, 2019). The results identified that the VGG, Inception, and MobileNet-RF models accomplish worse results. At the same time, the MobileNet and KNN models have resulted in moderately improved performance. Meanwhile, the PSO algorithm has reached considerable performance with accu _y , prec _n , reca _l , and F _score of 98.66, 97.94, 97.78, and 97.76%, respectively. Nevertheless, the IFBFFA-NDL technique gains maximum outcomes with accu _y , prec _n , reca _l , and F _score of 99.73, 98.69, 98.71, and 98.69% respectively.

Table 3:

Comparative outcome of the IFBFFA-NDL approach with other systems.

Algorithm	Accuracy	Precision	Recall	F-score
IFBFFA-NDL	99.73	98.69	98.71	98.69
PSO algorithm	98.66	97.94	97.78	97.96
VGG	96.43	96.13	97.69	96.21
Inception	96.86	96.66	96.22	95.08
MobileNet	97.80	97.67	97.98	97.01
MobileNet-RF	96.00	97.98	95.48	97.16
KNN model	97.51	95.09	97.18	95.25

IFBFFA-NDL, Information Feedback Firefly Algorithm with Nested Deep Learning.

Figure 7:

Comparative outcome of the IFBFFA-NDL approach with other systems. IFBFFA-NDL, Information Feedback Firefly Algorithm with Nested Deep Learning.

CONCLUSION

In this manuscript, we have focused on the development of an automated gesture recognition model, named the IFBFFA-NDL model. The IFBFFA-NDL technique exploits the concepts of DL with a metaheuristic hyperparameter tuning strategy for the recognition process. It involves three processes such as NASNet feature extraction, IFBFFA-based parameter tuning, and NLSTM-based recognition. To generate a collection of feature vectors, the IFBFFA-NDL technique uses the NASNet model. For optimal hyperparameter selection of the NASNet model, the IFBFFA algorithm was used. To recognize different types of gestures, the NLSTM classification model is exploited. For exhibiting the improvised gesture detection efficiency of the IFBFFA-NDL technique, a detailed result analysis can be conducted and the results highlighted the improved recognition rate of the IFBFFA-NDL technique compared to recent approaches in terms of several measures. In future, advanced hybrid DL models can be used to improve the recognition rate of the proposed model.

CONFLICTS OF INTEREST

The authors declare no conflicts of interest in association with the present study.

REFERENCES

1. Adeel MI, Asad MA, Zeeshan MR, Amna M, Aslam M, Martinez-Enriquez AM. 2022 March. Gesture based confidence assessment system for visually impaired people using deep learningAdvances in Information and Communication: Proceedings of the 2022 Future of Information and Communication Conference (FICC); Vol. Volume 2. Springer International Publishing. Cham. p. 135–147

2. Al-Hammadi M, Muhammad G, Abdul W, Alsulaiman M, Bencherif MA, Mekhtiche MA. 2020. Hand gesture recognition for sign language using 3DCNN. IEEE Access. Vol. 8:79491–79509

3. Bastos IL, Melo VH, Schwartz WR. 2019 October. Multi-loss recurrent residual networks for gesture detection and recognition2019 32nd SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI); IEEE. Rio de Janeiro, Brazil. 28-31 October 2019; p. 170–177

4. Can C, Kaya Y, Kılıç F. 2021. A deep convolutional neural network model for hand gesture recognition in 2D near-infrared images. Biomed. Phys. Eng. Express. Vol. 7(5):

5. Deepa S, Umamageswari A, Menaka S. 2023. A novel hand gesture recognition for aphonic people using convolutional neural networkComputer Vision and Machine Intelligence Paradigms for SDGs: Select Proceedings of ICRTAC-CVMIP 2021; Springer Nature Singapore. Singapore. p. 235–243

6. Ehrnsperger MG, Brenner T, Hoese HL, Siart U, Eibert TF. 2020. Real-time gesture detection based on machine learning classification of continuous wave radar signals. IEEE Sens. J. Vol. 21(6):8310–8322

7. Gangrade J, Bharti J. 2023. Vision-based hand gesture recognition for Indian sign language using convolution neural network. IETE J. Res. Vol. 69(2):723–732

8. Islam MS, Jannat MKA, Hossain MN, Kim WS, Lee SW, Yang SH. 2023. STC-NLSTMNet: an improved human activity recognition method using convolutional neural network with NLSTM from WiFi CSI. Sensors. Vol. 23(1):356

9. Jiang S, Shang J, Guo J, Zhang Y. 2023. Multi-strategy improved flamingo search algorithm for global optimization. Appl. Sci. Vol. 13(9):5612

10. Jindal M, Bajal E, Sharma S. 2023. A comparative analysis of established techniques and their applications in the field of gesture detectionMachine Learning Algorithms and Applications in Engineering. p. 73

11. Jo YU, Oh DC. 2020. Real-time hand gesture classification using CRNN with scale average wavelet transform. J. Mech. Med. Biol. Vol. 20(10):2040028

12. Kocejko T, Brzezinski F, Polinski A, Ruminski J, Wtorek J. 2020 June. Neural network based algorithm for hand gesture detection in a low-cost microprocessor applications2020 13th International Conference on Human System Interaction (HSI); IEEE. Tokyo, Japan. 6-8 June 2020; p. 204–209

13. Kogilavani SV, Prabhu J, Sandhiya R, Kumar MS, Subramaniam U, Karthick A, et al.. 2022. COVID-19 detection based on lung CT scan using deep learning techniques. Comput. Math. Methods Med. Vol. 2022:7672196

14. Kraljević L, Russo M, Pauković M, Šarić M. 2020. A dynamic gesture recognition interface for smart home control based on Croatian sign language. Appl. Sci. Vol. 10(7):2300

15. Köpüklü O, Gunduz A, Kose N, Rigoll G. 2019 May. Real-time hand gesture detection and classification using convolutional neural networks2019 14th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2019); IEEE. Lille, France. 14-18 May 2019; p. 1–8

16. Mosavvar I, Ghaffari A. 2019. Data aggregation in wireless sensor networks using firefly algorithm. Wireless Pers. Commun. Vol. 104:307–324

17. Ozcan T, Basturk A. 2019. Transfer learning-based convolutional neural networks with heuristic optimization for hand gesture recognition. Neural Comput. Applic. Vol. 31:8955–8970

18. Sun Y, Fei T, Gao S, Pohl N. 2019 May. Automatic radar-based gesture detection and classification via a region-based deep convolutional neural networkICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); IEEE. Brighton, United Kingdom. 12-17 May 2019; p. 4300–4304

19. Varsha M, Nair CS. 2021 July. Indian sign language gesture recognition using deep convolutional neural network2021 8th International Conference on Smart Computing and Communications (ICSCC); IEEE. India. 01-03 July 2021; p. 193–197

20. Wang Y, Ren A, Zhou M, Wang W, Yang X. 2020. A novel detection and recognition method for continuous hand gesture using FMCW radar. IEEE Access. Vol. 8:167264–167275

21. Wu S, Li Z, Li S, Liu Q, Wu W. 2023 March. An overview of gesture recognitionInternational Conference on Computer Application and Information Security (ICCAIS 2022); SPIE. Vol. Vol. 12609. p. 600–606

22. Zhang J, Zeng X. 2022. Multi-touch gesture recognition of Braille input based on Petri Net and RBF Net. Multimed. Tools Appl. Vol. 81(14):19395–19413