Introduction
This natural inequality of the two powers, of population, and of production of the earth, and that great law of our nature which must constantly keep their effects equal, form the great difficulty that appears to me insurmountable in the way to the perfectibility of society (Malthus, 1798)
In the two centuries since Malthus highlighted the crisis of balancing food production with a growing population, the agricultural industry has successfully produced enough food to feed a global population that has increased eightfold (Evans, 1998; Federico, 2005). During the first 100 yr, 1800–1990, this success was achieved by increasing the amount of land cultivated (Evans, 1998). In the last 50 yr, the success of the agricultural sector is largely attributable to productivity growth (Federico, 2005). Not only has global agricultural production successfully produced enough food to feed a growing population, the real price of food has fallen and the amount of labour required for agricultural production has reduced significantly, releasing labour to other sectors of the economy (Federico, 2005; Fuglie et al., 2012).
Falling prices are an indication that, in economic terms, supply exceeds demand. However, in the last decade the nominal price of agricultural commodities has been increasing, an indication that the supply–demand relationship is changing. According to the International Monetary Fund (IMF), world prices of agricultural commodities, measured in inflation-adjusted US dollars, rose by approximately 63% between 2000 and 2011 (Fuglie et al., 2012). The decade-long trend of rising prices, and increasing environmental concerns in relation to climate change, has brought the age-old Malthusian dilemma about the limits of agriculture back into focus.
The relationship that agriculture has with the environment is unique. Environmental conditions such as soil quality and water supply determine “what” can be produced, “when” it can be produced and “how much” of it is produced (Federico, 2005). The main challenge facing the agricultural sector in the coming decades involve striking a balance between productivity growth and protecting our natural resources (Fuglie et al., 2012).
This paper, in identifying an appropriate measure of TFP for Irish dairying, addresses a number of policy issues. First, at an international level, productivity growth has been highlighted as an important factor in dealing with the challenges that face the global agricultural industry. According to Fuglie et al. (2012), the first step in assessing the prospects for future productivity growth is to understand the past. Identifying what drives productivity growth first involves developing ways to accurately measure productivity. This is by no means an easy task; farm-level heterogeneity, multiple farm inputs and multiple farm outputs complicate the task of measuring farm-level productivity. “Measuring Productivity is a process that requires great care due to conceptual, methodological and data issues” (Matthews, 2014).
The European Innovation Partnership for Agricultural Productivity and Sustainability (EIP–AGRI), launched by the European Commission in 2012, has as an objective promoting a “resource efficient, productive… and resilient agricultural sector” by fostering a competitive and sustainable agriculture and forestry sector that “achieves more from less”. The research in this paper represents a key component for assessing the productivity performance of Irish agriculture. The data used are farm accountancy data supplemented by agricultural input and output price indices and the methodology closely follows the Organisation for Economic Co-operation and Development (OECD) manual for agricultural productivity measurement (OECD, 2001).
The principal motivation for this research is to develop a measure of agricultural productivity that helps us understand whether sustainable economic growth is being achieved, that is, growth that delivers improved incomes to farmers, and this requires a measure of the TFP performance. Decisions concerning the utilisation of agricultural resources can be informed by examining the comparative TFP growth performance of the main sectors of Irish agriculture. Such informed decision-making (at farm, industry and policy levels) could contribute to a more efficient use of resources and to the economic and general environmental sustainability of Irish agriculture.
This paper will proceed as follows: the second section provides a brief discussion about the definition of productivity and reviews previous research that has examined the TFP of Irish agriculture. The third section outlines the different methods of measuring TFP. The fourth section discusses traditional index number methods and introduces the Fisher index approach that is applied in this paper. The fifth section outlines the data and the specific input and output variables used in the Fisher index calculation of the TFP performance of Irish dairy farms. In the final section, we present the results and conclusions.
What is productivity
Productivity is a measure of how efficiently inputs are combined to produce outputs and is defined as the ratio of the volume (quantity) of inputs to the volume (quantity) of outputs (Coelli et al., 2013). The most informative measure of agricultural productivity is total factor productivity (TFP). Total factor productivity measures relate the output to a bundle of inputs such as capital, labour, land and intermediate inputs (OECD, 2001). Total factor productivity takes into account all of the land, labour, capital and intermediate resources employed in farm production and compares these with the total amount of crop and livestock output produced. If the total quantum of output produced is growing at a faster rate than the total quantum of inputs used, we call this an improvement in TFP (“factor” = input). Total factor productivity can increase, decrease or stay the same depending on the changes in inputs or outputs (see Table 1).
How productivity changes
| Increase in productivity | Decrease in productivity | Unchanged productivity | |||
|---|---|---|---|---|---|
| • | Output increases: input decreases or remains unchanged | • | Output decreases: input increases or remains unchanged | • | Both output and input remain unchanged |
| • | Both output and input increase, but output increases at a faster rate | • | Both output and input decrease, but output decreases at a faster rate | • | Both output and input increase/decrease at the same rate |
| • | Both output and input decrease, but output decreases at a slower rate | • | Both output and input increase, but output increases at a slower rate | ||
Source: Adapted from Zhao et al. (2012).
Total factor productivity differs from partial productivity measures such as crop yield per hectare or agricultural value added per worker because it takes into account the full set of inputs used in production. Thus, a TFP index reflects the output per unit of some combined set of inputs, so an increase in TFP reflects a gain in the output quantity, which is not originating in an increase of input use. Total factor productivity reveals the joint effects of many factors including new technologies, economies of scale, managerial skill and changes in the organisation of production (Petrick & Kloss, 2018). Partial productivity of the individual components of TFP, land labour and capital can also be an indicator of the contribution of these different components of TFP to the total output. Partial productivity measures are calculated as follows:

Figure A1 in the Appendix shows these partial productivity indicators.
Total factor productivity is therefore an indicator of the long-term performance of the agricultural industry as a whole in terms of how efficiently inputs are turned into output. As the EU agricultural policy continues to become more market-orientated and simultaneously more focused on the environment, growing agricultural incomes, maintaining the environmental sustainability of Irish agriculture will require increased emphasis on improving the productivity performance of the Irish agricultural sector. In this paper, we focus on measuring the TFP performance of Irish dairy farms between 2006 and 2016.
While the concept of productivity growth is reasonably straightforward and well defined in theory, choosing an appropriate method to measure it is not (Fuglie et al., 2012). Although TFP growth is generally understood to reflect the difference between the growth rate of total output and the growth rate of total input, there is no universally accepted method for its measurement. The four main empirical methods are: (i) econometric estimation of deterministic production frontiers; (ii) econometric estimation of stochastic production frontiers; (iii) data envelopment analysis (DEA); and (iv) conventional index methods (Zhao et al., 2012).
Methods of measuring TFP
Frontier-based methods of measuring TFP
Econometric estimation of deterministic production frontiers estimates the technical relationship that transforms the main categories of inputs into technically efficient (best practice) levels of outputs. Deterministic models assume that farms are technically efficient, that is, that there is a level of production that cannot be exceeded (the production frontier) but that some farms may not attain this level of production. The residual of the regression equation, which represents the level of output not explained by the level of inputs, can then be used as an estimate of TFP (Pozzi & Schivardi, 2016).
The econometric estimation of stochastic production frontiers uses econometric regression techniques to estimate the best practice or technology frontier for a set of farms. Econometric estimation methods such as stochastic frontier analysis (SFA) can accommodate data noise as a symmetric error term in defining the production frontier. In SFA, a one-sided error term is included representing technical inefficiency. These are farms that are not operating on the production frontier due to farm production decisions of the farmer rather than measurement error in the data. While methods that use econometric regression techniques allow for the production function to be fully represented by so-called flexible functional forms and can accommodate data noise, econometric issues may reduce the robustness of the estimates (Diewert, 1986). Econometric techniques are also not suitable where the regular updating of TFP estimates are desired, as this requires the re-estimation of a large system of equations.
Data envelopment analysis uses linear programming techniques to locate the production frontier for a set of farms. Both DEA and SFA methods allow for the observed change in TFP to be decomposed into changes in technology, that is, a shift in the location of the production frontier, and changes in the degree of inefficiency, that is movement towards or away from the production frontier (Zhao et al., 2012). However, because DEA uses linear programming techniques to locate the production frontier, DEA methods are unable to accommodate noise in the data, and outliers that can result from measurement error may result in erroneous assessment of production frontier locations and implied productivity performance (Zhao et al., 2012).
Conventional index methods
Index number approaches to measuring productivity have traditionally been applied to the study of agricultural productivity because of the ease with which they can be calculated and updated and because they allow for comparisons of changes in TFP performance over time and between different sectors or countries (OECD, 2001). Conventional index methods of measuring productivity require data on the prices and quantities of each input and each output used in the production process, but only two observations are necessary to construct an index. Compared to econometric, SFA and DEA methods of measuring TFP, the data requirements for conventional index methods are less onerous. It is also unnecessary to make any assumptions about the parameters or form of the underlying production technology when using index methods.
Total factor productivity growth measured using index number methods includes the contributions of technological change, improvements in efficiency and other sources of productivity improvements such as economies of scale and the more efficient use of existing capacity (Zhao et al., 2012). Until recently, decomposition of TFP using conventional index number methods was a problem; however, recent contributions to the literature show that by combining an index number formula with estimation techniques, it is possible to decompose the Fisher Ideal index (Kuosmanen & Sipiläinen, 2009), the Lowe index (O’Donnell, 2012) and the Bennet–Lowe indicator (Ang, 2019).
Agricultural production generally involves multiple inputs and outputs, and farm-level datasets provide a rich source of financial, socioeconomic and demographic data. Index number methods are particularly useful in summarising and reducing this overwhelming abundance of microeconomic information. Hence, index numbers intrude themselves on virtually every empirical investigation in economics (Diewert, 1986).
The appropriate method to use when calculating measures of agricultural TFP will depend on a number of factors, including (i) the data available, (ii) the end use of the productivity estimates, and (iii) whether it is important to accommodate noise in the data such as measurement error or omitted inputs or outputs (Zhao et al., 2012). Index number methods are the most commonly used instruments to measure changes in the levels of various economic variables (Coelli et al., 2005). According to Fisher (1922), the fundamental purpose of an index number is that it should fairly represent, in as far as one single figure can, the general trend of the many diverging ratios from which it is calculated. While the concept of agricultural TFP is reasonably straightforward, using the index method to measure it in practice is still a challenging task (Zhao et al., 2012).
Agricultural TFP estimates using a traditional index methodology were first developed by the Economic Research Service of the US Department of Agriculture (Ball, 1985; Ball et al., 1997, 2002; Fuglie et al., 2007). To date, the methods developed in by the ERS-USDA have been replicated by many countries (Thirtle & Bottomley, 1992; Coelli, 1996; Darku et al., 2016). International comparisons are regularly carried out using these methods (Fuglie, 2010; Fuglie et al., 2012; Sheng et al., 2013). Recent Irish studies of agricultural productivity and efficiency include O’Neill & Matthews (2001), Thorne (2004), Matthews et al. (2006), Gillespie et al. (2015) and Cillero et al. (2018); however, only two previous studies, Boyle (1987) and Matthews (1999/2000), have used an index number approach to measuring agricultural TFP. Both Boyle (1987) and Matthews (1999/2000) used aggregated national accounts data to calculate a measure of TFP for the Irish agricultural industry as a whole. This paper adds to their work by developing a measure of agricultural TFP using micro farm-level data and a Fisher Ideal index method. This method is capable of providing a measure of the overall TFP performance of the Irish agricultural industry, as defined by the National Farm Survey (NFS) sampling frame, while also taking into account the heterogeneous nature of Irish agriculture and providing a measure of TFP at a sectoral level. An important consideration for the development of this measure is that it is capable of being updated on a regular basis using annual NFS data and the Irish Central Statistics Office (CSO) data.
The remainder of this paper focuses on issues that are specific to the use of a conventional index methodology in the measurement of the TFP performance of Irish agriculture (specifically Irish dairy farms) using farm-level NFS data supplemented where necessary by national price indices. The NFS dataset makes it possible to produce detailed estimates and analyses of productivity, and of the factors influencing productivity, at the farm, sector and national aggregate levels. The methodology used in this paper closely follows that utilised by the Australian Bureau of Agricultural and Resource Economics and Sciences (ABARES) in its measurement of the TFP performance of the Australian Broadacre and dairy industries. The ABARES approach uses farm-level records collected by its farm survey programme and applies OECD guidelines to productivity measurement as set out in the productivity manual (OECD, 2001; Gray et al., 2010).
Choosing the most appropriate index number
In the literature on index number theory, two approaches are used to select and assess the quality of an index formula. The first method is the axiomatic test method developed by Fisher (1922). This method tests index number formulae for a number of desirable mathematical properties. Index formulae that pass more axiomatic tests are considered to be superior to or “ideal” in comparison to other aggregation methods (Fisher, 1922). Fisher outlined eight requirements which he considered desirable for an index number and carried out axiomatic tests on 134 formulae to determine which passed and which did not.1 Of the 134 formulae tested, Fisher identified the geometric mean of the Laspeyres and Paasche indices as the formula which passed the most tests and this index formula is now known as the Fisher Ideal index.
The second approach used to determine the precision of an index number formula is the economic theory approach (Diewert, 1976; 1981). Under this approach, the microeconomic theory provides the rationale for choosing between different aggregation methods. A superlative quantity index is an index number formula which is consistent with a consumer or producer maximising a “flexible” aggregator function (production/utility function) subject to a budget or resource constraint. A “flexible” functional form is one which can provide a second-order approximation to an arbitrary function (Diewert, 1976). Diewert (1976) shows that the Fisher Ideal index provides an exact representation for an underlying quadratic functional form of production technology, while the Törnqvist index provides an exact representation of an underling translog functional form. The following section outlines the specific characteristics of both the Fisher Ideal and Törnqvist indices and the Laspeyres and Paasche indices on which they are based.
Laspeyres index
The Laspeyres quantity index uses base period prices as weights and is defined as follows:
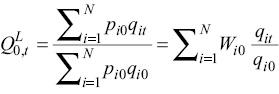
where
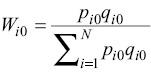
Paasche index
The Paasche quantity index uses current period prices as weights and is defined as follows:

where
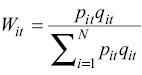
Fisher Ideal
The Fisher Ideal index is the geometric mean of the Laspeyres and Paasche indices, and is defined as follows:
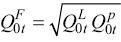
Chained Fisher index
When a Fisher index is calculated between two time periods, for example between period 0 and period 2, the direct Fisher index is calculated as follows:

However if we include the intervening period (period 1) in the calculation, the Fisher index now becomes:
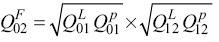
Both the direct and chained indices measure the same thing but they are likely to give different values (Zhao et al., 2012). Alternatively, the indices can be linked together over a longer time period, for example the CSO uses a Laspeyres fixed base index which updates the base year at five yearly intervals.
Törnqvist
The Törnqvist index is a weighted geometric average of the price relatives, with weights given by the simple average of the value share in periods 0 (base) and t (current).
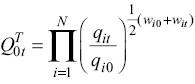
However, the Törnqvist index is usually presented and applied in its log-change form:
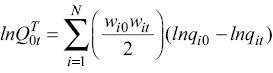
Choosing between the Fisher Ideal and the Törnqvist is difficult as both formulae adhere to a number of critical tests and criteria, and according to the OECD (2001) the choice between the two matters little. An empirical investigation of the effects of using different formulae to compile an index of Irish agricultural output over the period 1960–1982 found that the index values were relatively insensitive to the index formula chosen (Boyle, 1988). However, as this project will use farm survey data, the aggregation method applied to measure the TFP performance needs to be able to accommodate zero values, which are a typical feature of survey data. Because of this important operational consideration, the Fisher Ideal index is more appropriate than the Törnqvist index which (because of its logarithmic form) cannot handle zero values.
While the main advantage of using the Fisher Ideal index is that it is easy to commute whilst remaining consistent with the economic theory, it may be sensitive to outliers, as is the case with DEA. To correct for any bias arising from a potential outlier, a visual check using a simple graph box is carried out after each individual calculation. If the variable seems to include an outlier, it is investigated further and dropped from the dataset if necessary.
Multilateral Fisher index
While the Fisher Ideal index satisfies many of the axiomatic tests, it fails the circularity or transitivity test (Coelli et al., 2005). Transitivity implies that a comparison between any pair of farms is internally consistent and that a direct comparison of any two farms should be the same as a possible indirect comparison through a third farm. Transitivity requires that for any three farms A, B and C,
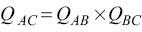
In order to generate the transitive Fisher index, the Elteto–Koves–Szulc (EKS) method in Equation 9 is applied, and the quantity index number
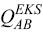
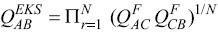
Measuring Irish Agricultural TFP using NFS farm-level panel data
Farming systems: how farms are classified
The data used for this research is the Teagasc NFS data which is collected annually and weighted to be representative of the Irish national farming population. Within the NFS, farms are classified into six farm systems based on the dominant enterprise on the farm. From 1996 to 2009, farms were classified into farm systems on the basis of standard gross margin (SGM). An SGM was assigned to each type of farm animal and each hectare of crop on the farm. Farms were then classified into systems on the basis of the most dominant enterprise on the farm according to the SGM measure. From 1996 to 2009, the farm systems were as follows: Dairying, Dairying + Other, Cattle Rearing, Cattle Other, Mainly Sheep and Tillage.
In 2010, the method of classifying farms changed to the standard output (SO) method. Due to the decoupling of direct payments, a negative SGM was possible making it difficult to classify some farms (Hennessy et al., 2010). Farms are now classified on the basis of the output of the farm rather than the gross margin. Direct payments are not included in SO and the Dairying and Other system has been replaced by the Mixed Livestock system. Farms are assigned to these systems as per the EU farm typology, and in the case of mixed holdings the dominant enterprise on the farm is identified by whichever enterprise contributes two-thirds of the overall SO of the farm. In this study, a dairy farm is defined as a farm where two-thirds of the farm’s SO originates from the dairy enterprise (Dillon et al., 2016). This system definition acknowledges that there may be other enterprises (and associated outputs) on a farm defined as a dairy farm; this means that in the calculation of the TFP of dairy farms, all farm outputs are included as explained in the following section.
Output and input measures
The main source of the individual output and input data variables used to construct the Fisher output and input indices is the Teagasc NFS supplemented where necessary with CSO data2. To construct the output and input indices, which are the main building blocks for the overall TFP index, information on prices and quantities in at least two time periods is required. Where data are available on the physical quantities and the total value of a single input or output, the following equation is used to derive prices.
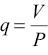
where q is the quantity measure, V is the total value and P is the price per unit of q, and therefore p is equal to total value/quantity. Where only V, the total value of the output or input, is available, CSO data on agricultural price indices are used for P and Equation 10 is used to derive a quantity measure.
Gross output versus value-added estimates of TFP
The final consideration in calculating an estimate of TFP is whether to use an output measure based on value-added or a measure based on the gross output. A value-added measure excludes intermediate inputs (materials, energy and services used up in the process of production), while the gross output measure includes those inputs. In the former measure, a value-added output measure is related to capital and labour as inputs; in the latter, the gross output is related to capital, labour and intermediate inputs. Productivity in the gross output formulation is
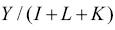
where Y is the gross output, I is the intermediate input use, L is the labour input and K is the capital input. Productivity in the real value-added framework is roughly
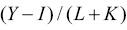
For a productivity improvement of ΔY with all inputs remaining constant, the gross output productivity growth rate is

This is less than the real value-added productivity growth rate.
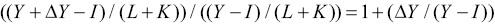
Thus, the smaller denominator in the value-added TFP measure translates into larger TFP growth measures.
The difference between the two concepts of productivity growth is less pronounced at the aggregate (or national) level than it is at the sectoral or industry level. At the aggregate level, gross output-based and value-added-based measures are close, only differing to the extent that intermediate inputs are sourced from imports. In proportional terms, this tends to be low (Cobbold, 2003). At the industry or sector level, however, intermediate usage tends to be a much higher proportion of gross output. This results in greater variation between the two measures (OECD, 2001; Cobbold, 2003).
Because intermediate services (materials and services) represent a significant proportion of total farm input expenditure at the farm level, and because technological change and new innovations may be embedded in these intermediate inputs as well as in capital and labour, or because technological change may lead farmers to choose new combinations of capital, labour, land and intermediate services, we adopt a gross output measure similar to the ABARES measure of TFP (Gray et al., 2010).
Output
The output set used includes all livestock, milk and crops produced and sold off of the farm. Each farm in the Teagasc NFS has information on the value of each type of output sold and associated quantities. Prices for each type of output are derived using Equation 10. Table 2 lists all output variables included in the calculation of a total output index for Irish dairy farms.
List of variables included in total output
| Dairy livestock | Dairy calves sold, dairy breeding animals sold, dairy-culled animals sold |
| Cattle livestock | Non-dairy calves sold, weanlings sold, stores sold, finished sold, breeding herd sold, cattle used in house, cattle other sales |
| Sheep livestock | Store lambs sales, fat hogget sales, breeding hogget sales, cull sales, breeding ewes sales |
| Milk output | Milk sold, milk fed to animals and milk used in the house |
| Crops output | Barley, wheat, oats, potatoes, straw |
Source: Teagasc National Farm Survey (NFS).
Table 3 presents a Fisher quantity index of the total output for Irish dairy farms for the period 2006–2016. Total output consists of the total quantity of milk and livestock and crops produced and sold off of the farm. Milk is the main driver of total output on dairy farms; livestock sold are mainly bull calves and as the main focus of dairy farms is to produce milk, these animals are of low value. Heifer calves, on the other hand, have a higher value as replacement stock, and are retained on many Irish dairy farms. Replacement dairy heifers are represented in the data on the input side as transfers into the farms’ livestock inventory.
Total outputs, Irish dairy farms 2006–2016 (2010 = 100) N = 1,322
| Year | Fisher total output | EKS Fisher total output | Livestock output | Milk output | Crops output | CSO milk price index | CSO cow numbers index | Milk output per cow index |
|---|---|---|---|---|---|---|---|---|
| 2006 | 103.7 | 110.4 | 113.7 | 98.6 | 86.3 | 90.0 | 101.0 | 102.7 |
| 2007 | 102.6 | 105.7 | 112.4 | 100.0 | 86.5 | 112.0 | 102.0 | 102.3 |
| 2008 | 98.7 | 97.2 | 100.4 | 97.2 | 121.2 | 111.0 | 102.0 | 99.8 |
| 2009 | 94.7 | 94.8 | 94.1 | 97.7 | 77.0 | 102.0 | 97.2 | |
| 2010 | 100.0 | 100 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| 2011 | 103.9 | 104.3 | 114.1 | 103.6 | 82.9 | 114.0 | 104.0 | 101.6 |
| 2012 | 103.2 | 100.5 | 113.8 | 102.6 | 91.4 | 104.0 | 107.0 | 99.1 |
| 2013 | 108.6 | 103.1 | 118.0 | 108.7 | 110.0 | 127.0 | 109.0 | 102.6 |
| 2014 | 113.9 | 115.4 | 128.9 | 112.6 | 125.0 | 122.0 | 115.0 | 101.9 |
| 2015 | 125.1 | 121.8 | 129.0 | 127.2 | 127.3 | 95.0 | 121.0 | 106.6 |
| 2016 | 130.9 | 126.6 | 135.6 | 133.9 | 124.1 | 87.0 | 131.0 | 108.2 |
Source: Author’s own derivation based on Teagasc NFS and CSO Agricultural Price Indices.
CSO = Central Statistics Office; EKS = Elteto–Koves–Szulc; NFS = National Farm Survey.
The base year used for all indices is 2010; this base was chosen because the CSO uses a Laspeyres index to calculate the agricultural input and output price index and this index is updated at 5-yr intervals, with the most recent update to a 2010 base. The CSO price indices are used for some calculations on the input side of the TFP measurement where the relevant price index is used to derive quantities that are not available from the Teagasc NFS dataset.
Multilateral comparisons are based on the EKS Fisher total output calculation which maintains the internal consistency necessary for these comparisons (OECD, 2001; Coelli et al., 2005; Zhao et al., 2008). Relative to 2010, there has been a 26.6% increase in the total output of Irish dairy farms, the largest year-on-year increase took place between 2013 and 2014 when the total dairy farm output increased by 12%. Since milk quotas were removed in April 2015, the total output on Irish dairy farms has increased by a further 10%. The trends in total dairy farm output are broadly in line with the trends in dairy cow numbers as measured by the CSO and show that Irish dairy farmers had been increasing cow numbers in anticipation of the removal of the quota so as to be in a position to increase milk production once the quota system was removed. Milk output has increased by 34%, which is higher than the increase in cow numbers and is reflective of the increase in productivity of 8% per cow.
The milk price index in Table 3 is taken from the CSO agricultural input and output price index dataset (CSO, 2017), and the dairy cow numbers index are derived from CSO data on dairy cow numbers. These indices are included here for reference only and to provide some background for the Fisher total output index calculated using the farm-level Teagasc NFS data.
Inputs
The input side of the calculation of agricultural TFP includes all of the factors involved in producing output on the farm, namely land, labour, capital (fixed and live) as well as materials and services.
Land
To construct a quantity index for land as an input into the production process, we use the utilised agricultural area (UAA) of the farm hectares reported in the Teagasc NFS. The UAA includes the area under crops and pasture plus the area of rough grazing. It is the total area owned, plus the area rented in, minus area let out, minus area under remainder of the farm (buildings, farmyard woodlands, etc.). The weight applied to this quantity measure in the calculation of the associated Fisher Ideal index is the opportunity cost of the land which is taken as equal to the per-hectare rental price of land rented in. This information is collected annually in the Teagasc NFS. However, not all farmers rent land in and so for those farms without land rented in, an average per-hectare rental price is imputed based on the average rental price paid by farms in that farm system (Appendix Table A1). Thus, for a dairy farm without land rented in, the opportunity cost of their land is taken as equal to the average rent paid for land rented in by all farms classified as dairy farms. This means that the imputed opportunity costs for dairy farm land will differ from that imputed for land used by farms classified as Tillage, Cattle Rearing, Cattle Other and Sheep Farm farms.
Labour
Labour input consists of two items: hired labour (paid labour) and family labour (unpaid labour). The quantity of paid and unpaid labour on each farm is measured in hours, which the NFS also converts to annual work units (AWU) with one AWU being defined as 1,800 h or more of labour per person per annum (Dillon et al., 2016). No one person can be more than one labour unit, even if the farmer reports that they work more than 1,800 h/yr. In this study, the total hours worked by both family labour and hired labour is preferred to AWU and the quantity of labour is the sum of both hired and family labour hours.
The price of labour is typically the wage rate, but Irish farmers do not pay themselves a wage; therefore, accounting for the price of labour is a challenging issue. In this study, we have used Agricultural Output, Input and Income CSO data to construct a labour price index based on the “Compensation of Employees” data (Table 4).
Labour price index based on CSO data
| Year | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Compensation of employees (Euro Million) | 425 | 449 | 436 | 428 | 465 | 475 | 468 | 491 | 496 | 489 | 508 |
| Labour price index | 92 | 97 | 94 | 92 | 100 | 102 | 101 | 106 | 107 | 105 | 109 |
Source: CSO.
CSO = Central Statistics Office.
Both hired and family labour hours are weighted by the labour price index and while we acknowledge that there are limitations to this methodology3, the absence of a farm labour wage rate necessitates such a construct.
Capital
The measurement of the capital inputs used in production required the measurement of the flow of services provided by each capital component rather than with the stock of capital per se. Capital input flows are not directly observable but are assumed to be proportional to the capital stock. The capital stock is the current market value of the productive capital stock, adjusted for deprecation of the capital asset (OECD, 2001). For fixed capital items (farm buildings, plant and machinery), the Teagasc NFS contains information on the end-of-year valuation of fixed assets. A fixed capital quantity variable is derived by dividing the value of the fixed asset variable from the NFS by the relevant price index in CSO; for example, the value of farm buildings is weighted by the “building and construction (i.e. materials and wages)” price index produced by the CSO.
A quantity for the flows of services from machinery capital is similarly derived using the CSO price index for “transportable capital for use in agriculture” and the end-of-year valuation of machinery from the Teagasc NFS (FADN, 2013).
Capital livestock inputs are the quantity of animals purchased during the year in question. The Teagasc NFS dataset contains information on the number and the value of livestock purchased in by farms; Equation 13 is then applied to derive prices. Livestock purchased in include dairy animals, other cattle and sheep. Table 5 describes all animal types included in the livestock capital input variable.
List of animal types included in livestock capital input
| Dairy livestock | Dairy cows, springing heifers and breeding bulls purchased |
| Cattle livestock | Calves, weanlings, stores, breeding herd and other cattle purchased |
| Sheep livestock | Store lambs, breeding hoggets, ewes and ram purchased |
Source: NFS.
NFS = National Farm Survey.
It is also necessary to capture the value added to the herd during the year through the natural maturing of animals. To account for this natural process, the capital value of the herd is measured as the opening valuation plus the closing valuation of the livestock stock divided by 2. As there is no way of differentiating this figure by individual animal types, the units of the quantity measure used in the Fisher index calculation is livestock units and the prices are derived by dividing the capital value of the herd by the total number of livestock units.
Intermediate services
To construct a quantity index for intermediate services used in Irish agricultural production, we use the value of direct and overhead costs as calculated in the Teagasc NFS dataset and prices from the CSO Agricultural input price index dataset (CSO, 2017) to derive quantities using Equation 13. Where appropriate price indices are available in CSO data for the individual components of NFS direct costs, a separate quantity index is calculated for each item (CSO, 2017).
Direct costs include purchases of concentrates and bulky feed, fertiliser, crop protection, seed, expenditure on machinery hire, transport services, livestock maintenance, casual labour and other miscellaneous livestock expenses. From this list, individual quantity indices are calculated for purchased feed, fertiliser, seed and transport services. These items are then removed from the aggregated NFS direct costs figure and the residual direct costs are weighted by the CSO agricultural input price index.
Teagasc NFS overhead costs include expenditure on cars, electricity and telephone costs, interest payments (including hire purchase payments), machinery-operating expenses, building repair and upkeep, general land maintenance, costs of lease of machinery, annuities, and other miscellaneous overhead costs.
The calculation of quantity indices for overhead costs is conducted in an analogous fashion to the calculation of quantity indices for direct costs; where appropriate individual indices are available from the CSO agricultural price indices dataset, an individual quantity index is calculated for the particular item. These items are then removed from the aggregated Teagasc NFS overhead costs figure and the residual is weighted by the agricultural input price index. From the list of Teagasc NFS overhead costs, individual quantity indices are calculated for the farm’s use of electricity, and the farm’s share of car and machinery-operating expenses are included in the overall farm transport index and weighted by the “transportable capital for use in agriculture” price index from the CSO. Table 6 presents the EKS Fisher quantity index of total input for Irish dairy farms during 2006–2016.
Total inputs, Irish dairy farms 2006–2016 (2010 = 100) N = 1,322
| Year | Fisher total input | EKS Fisher total inputs | Land | Labour | Fixed capital | Live capital | Intermediate services |
|---|---|---|---|---|---|---|---|
| 2006 | 101.2 | 101.8 | 95.3 | 105.8 | 101.8 | 108.4 | 95.5 |
| 2007 | 101.1 | 100.3 | 96.5 | 103.9 | 108.9 | 105.9 | 96.1 |
| 2008 | 101.5 | 100.5 | 97.4 | 104.5 | 117.4 | 106.5 | 94.2 |
| 2009 | 99.1 | 97.3 | 97.8 | 101.9 | 92.3 | 101.0 | 92.7 |
| 2010 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| 2011 | 101.7 | 101.9 | 102.7 | 101.9 | 98.4 | 108.1 | 98.9 |
| 2012 | 103.1 | 101.4 | 103.1 | 100.8 | 111.9 | 110.1 | 106.9 |
| 2013 | 107.6 | 104.4 | 104.4 | 103.6 | 118.7 | 114.7 | 118.4 |
| 2014 | 108.4 | 106.8 | 106.2 | 106.8 | 117.8 | 114.5 | 114.3 |
| 2015 | 109.6 | 106.2 | 107.8 | 107.2 | 111.7 | 125.5 | 112.8 |
| 2016 | 110.4 | 108.4 | 110.8 | 106.6 | 109.4 | 128.2 | 115.5 |
Source: Author’s own derivation based on Teagasc NFS data.
EKS = Elteto–Koves–Szulc; NFS = National Farm Survey.
Since 2010, there has been an increase of 8.4% in the total quantity of inputs. The flow of services from fixed capital, which includes buildings and machinery, has increased by 9.4% and the quantity of live capital has increased by 28%. Intermediate services used by Irish dairy farms have increased by 15% and labour has increased by 6%. Land is represented as the opportunity cost, that is, the cost of land rented in, and has steadily increased throughout the entire period with a 10% increase since 2010.
Total factor productivity
In this study, the total factor productivity is calculated as a gross output measure and is the ratio of an index of the total output to an index of the total input (Equation 15).

Table 7 presents the results of TFP4, total output5 and total input for Irish dairy farms during 2006–2016 and the transitive EKS Fisher measures of the total output, input and TFP, where the base year is 2010.
TTFP, total output and total inputs on Irish dairy farms 2006–2016 (2010 = 100) N = 1,322
| Year | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TFP | 102.7 | 102.1 | 97.6 | 96.2 | 100.0 | 102.4 | 100.5 | 101.6 | 106.2 | 115.6 | 119.9 |
| Total output | 103.7 | 102.6 | 98.7 | 94.7 | 100.0 | 103.9 | 103.2 | 108.6 | 113.9 | 125.1 | 130.9 |
| Total input | 101.2 | 101.1 | 101.5 | 99.1 | 100.0 | 101.7 | 103.1 | 107.6 | 108.4 | 109.6 | 110.4 |
| EKS TFP | 108.6 | 105.6 | 97.0 | 97.5 | 100.0 | 102.4 | 99.1 | 98.7 | 108.4 | 115.4 | 117.8 |
| EKS Total output | 110.5 | 105.7 | 97.3 | 94.8 | 100.0 | 104.3 | 100.5 | 103.1 | 115.4 | 121.8 | 126.6 |
| EKS Total Input | 101.8 | 100.3 | 100.5 | 97.3 | 100.0 | 101.9 | 101.4 | 104.4 | 106.8 | 106.2 | 108.4 |
Source: Author’s own derivation based on Teagasc NFS.
EKS = Elteto–Koves–Szulc; NFS = National Farm Survey; TFP = total factor productivity.
Our results show that since 2010, TFP on Irish dairy farms has increased by almost 18%, the total output has increased by 26.6% in line with the expansion in herd size on dairy farms and total inputs have increased by 8.4%. Further data from the Teagasc NFS shows that over the full period under analysis, the family farm income (FFI) on specialist dairy farms also increased, from approximately €34,000 in 2006 to just over €54,000 in 2016. Deregulation in the dairy industry with the removal of production quotas which have been in place since 1984 may explain the large increase in total output between 2013 and 2015 and although TFP continued to grow at a rate of 2.4% in 2016, the largest increase in TFP of almost 17% occurred in the years 2013–2015, and a longer series will be required to investigate the matter further. However, the purpose of this paper is to develop a methodology to measure TFP on a regular basis once NFS data become available.
Discussion
In this paper, we have outlined a methodology for measuring agricultural TFP at the farm, sector and industry level using the farm-level micro data. This research addresses the direction provided for in the recent policy reforms of the EU CAP, which has placed increased emphasis on the importance of productivity measurement and monitoring. We have applied a methodology recommended by the OECD manual on measuring productivity, a method also adopted by ABARES to measure TFP of Broadacre acre6 farms in Australia (OECD, 2001; Gray et al., 2010). Estimates show that on Irish dairy farms, TFP has increased by almost 18% in the years 2010–2016 and the majority of this growth occurred between 2013 and 2016. Dairy TFP has continued to grow by 2.5% in the production year 2016; it would seem therefore that the removal of the European dairy quota system has resulted in a windfall gain for Irish dairy farmers but that productivity gains are continuing.
Total factor productivity estimates measured in this way capture the net effect of a number of factors that cause productivity to change. These factors can be broadly defined as (i) new knowledge and technological progress, (ii) institutional or regulatory changes and (iii) structural changes at the farm level (Zhu & Lansink, 2010). These factors are not mutually exclusive and cover a broad range of actions and behaviours that can influence productivity growth on individual farms such as investment in new farm machinery or improved farmer ability through agricultural education or extension services and farmer innovation (Läpple et al., 2015; Läpple & Thorne, 2019).
Until recently, traditional index methods of estimating TFP could not identify individual drivers of productivity growth; rather, a TFP index measured the combined effect of multiple drivers. The removal of production quotas in 2015 is a significant development, and the full effects at the farm level continue to be investigated. Current research has found a statistically significant increase in the Irish dairy herd size following deregulation, but also that dairy farmers who were more productive prior to the abolition of quotas experienced a more positive impact from milk quota elimination (Zeng et al., 2017). However, it should also be noted that short-term factors such as price shocks, weather shocks, diseases, and so on can lead to variations in TFP calculations. As a result, the interpretation of year-to-year movements in TFP estimates is not straightforward. Future work will focus on identifying factors driving both cross-sectional and inter-temporal TFP growth of Irish agriculture.
Finally, given that the rationale for the completion of this research was embedded in the advances that must be met in achieving sustainable intensification goals within agriculture, this paper contributes to the body of knowledge that is required to measure sustainability at the farm level which includes measures of social, economic and environmental sustainability. This research has documented the shift in TFP over the recent past, along with economic sustainability improvements in the dairy sector associated with farm income improvements. From a policy perspective, the aforementioned changes in economic sustainability and productivity are important as pressures on agricultural resources increase due to increasing global food demand, whilst there is increased competition for the factors of production. Future work will involve linking this indicator of economic sustainability with the environmental and social sustainability indicators already developed within the Irish NFS (Hennessy et al., 2013).






